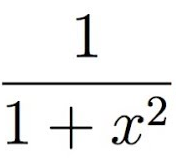PythonのJITがすごい
linux + python + opencvでロゴ検出類似度であれこれしようとしてるときに
pythonのNumbaのjitがすごい!みたいな記事を見かけたので試してみました。
とりあえず試してみる
プログラミングは専門外なので詳しくないですが
from numba import jit ,njit
from numba import prange
@jit()
def function4():
hoge
return
defの前に@jitをつけるだけ。
結果(N=10**8)
| エントリー | 時間 |
|---|---|
| C | 2.45秒 |
| func1 | 28.00秒 |
| func2(1+jit) | 3.09秒 |
| func3 | 32.8秒 |
| func4(3+jit) | 1.41秒 |
| func5(3+jit+prange) | 0.66秒 |
| func6(numpy) | 2.67秒 |
@jitつけるだけでお手軽で速すぎなのでは。
pythonのループは遅い(とくにfor)ってきいてたけどデフォは確かに遅かった。
numpyはよく分かってないのでこれでいいのかは不明。
間違いがあれば教えてください。
使ったもの1
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
int main(void){
long int i;
long int count = 0;
long int max = pow(10,8);
double x,y,pi;
clock_t start,end;
srand(time(NULL));
start = clock();
for(i=0;i<max;i++){
x = (double)rand()/RAND_MAX;
y = (double)rand()/RAND_MAX;
if(y<1/(1+x*x))
count++;
}
pi = (double)count / max * 4;
end = clock();
printf("%f\n", pi);
printf("%.2f秒かかりました\n",(double)(end-start)/CLOCKS_PER_SEC);
return 0;
}
使ったもの2
#!/usr/bin/python3
# -*- coding: utf-8 -*-
import time
import random
import numpy as np
from numba import jit ,njit
from numba import prange
N=10**8
def function1():
A=[1 if 1/(1+(random.random())**2) > random.random() else 0 for i in range(N) ]
ans=4*A.count(1)/N
return
@jit
def function2():
A=[1 if 1/(1+(random.random())**2) > random.random() else 0 for i in range(N) ]
ans=4*A.count(1)/N
return
def g(x):
return 1.0/(1.0+x**2)
def function3():
count = 0
for i in range(N):
x ,y= random.random(),random.random()
if y < g (x):
count +=1
ans=4*count/N
print(ans)
return
@jit('f8(f8)')
def f(x):
return 1.0/(1.0+x**2)
@jit()
def function4():
count = 0
for i in range(N):
x ,y= random.random(),random.random()
if y < f(x):
count +=1
ans=4*count/N
print(ans)
return
@jit(nopython=True, parallel=True)
def function5():
count = 0
for i in prange(N):
x ,y= random.random(),random.random()
if y < f(x):
count +=1
ans=4*count/N
print(ans)
return
def function6():
x, y = np.random.rand(N), np.random.rand(N)
c = (y<1.0/(1.0+x**2) ).sum()
ans=4*c/N
print(ans)
return